Frações
O símbolo 
significa a:b, sendo a e b números naturais e b diferente de zero.
Chamamos:
de fração;
a de numerador;
b de denominador.
Se a é múltiplo de b, então é um número natural.
Veja um exemplo:
A fração 
é igual a 8:2. Neste caso, 8 é o numerador e 2 é o denominador. Efetuando a divisão de 8 por 2, obtemos o quociente 4. Assim, é um número natural e 8 é múltiplo de 2.
Durante muito tempo, os números naturais foram os únicos conhecidos e usados pelos homens. Depois começaram a surgir questões que não poderiam ser resolvidas com números naturais. Então surgiu o conceito de número fracionário.
Critérios de divisibilidade
Para alguns números como o dois, o três, o cinco e outros, existem regras que permitem verificar a divisibilidade sem se efetuar a divisão. Essas regras são chamadas de critérios de divisibilidade.
Divisibilidade por 2
Um número natural é divisível por 2 quando ele termina em 0, ou 2, ou 4, ou 6, ou 8, ou seja, quando ele é par.
Exemplos:
1) 5040 é divisível por 2, pois termina em 0.
2) 237 não é divisível por 2, pois não é um número par.
Divisibilidade por 3
Um número é divisível por 3 quando a soma dos valores absolutos dos seus algarismos for divisível por 3.
Exemplo:
234 é divisível por 3, pois a soma de seus algarismos é igual a 2+3+4=9, e como 9 é divisível por 3, então 234 é divisível por 3.
Divisibilidade por 4
Um número é divisível por 4 quando termina em 00 ou quando o número formado pelos dois últimos algarismos da direita for divisível por 4.
Exemplo:
1800 é divisível por 4, pois termina em 00.
4116 é divisível por 4, pois 16 é divisível por 4.
1324 é divisível por 4, pois 24 é divisível por 4.
3850 não é divisível por 4, pois não termina em 00 e 50 não é divisível por 4.
Divisibilidade por 5
Um número natural é divisível por 5 quando ele termina em 0 ou 5.
Exemplos:
1) 55 é divisível por 5, pois termina em 5.
2) 90 é divisível por 5, pois termina em 0.
3) 87 não é divisível por 5, pois não termina em 0 nem em 5.
Divisibilidade por 6
Um número é divisível por 6 quando é divisível por 2 e por 3.
Exemplos:
1) 312 é divisível por 6, porque é divisível por 2 (par) e por 3 (soma: 6).
2) 5214 é divisível por 6, porque é divisível por 2 (par) e por 3 (soma: 12).
3) 716 não é divisível por 6, (é divisível por 2, mas não é divisível por 3).
4) 3405 não é divisível por 6 (é divisível por 3, mas não é divisível por 2).
Divisibilidade por 8
Um número é divisível por 8 quando termina em 000, ou quando o número formado pelos três últimos algarismos da direita for divisível por 8.
Exemplos:
1) 7000 é divisível por 8, pois termina em 000.
2) 56104 é divisível por 8, pois 104 é divisível por 8.
3) 61112 é divisível por 8, pois 112 é divisível por 8.
4) 78164 não é divisível por 8, pois 164 não é divisível por 8.
Divisibilidade por 9
Um número é divisível por 9 quando a soma dos valores absolutos dos seus algarismos for divisível por 9.
Exemplo:
2871 é divisível por 9, pois a soma de seus algarismos é igual a 2+8+7+1=18, e como 18 é divisível por 9, então 2871 é divisível por 9.
Divisibilidade por 10
Um número natural é divisível por 10 quando ele termina em 0.
Exemplos:
1) 4150 é divisível por 10, pois termina em 0.
2) 2106 não é divisível por 10, pois não termina em 0.
Divisibilidade por 11
Um número é divisível por 11 quando a diferença entre as somas dos valores absolutos dos algarismos de ordem ímpar e a dos de ordem par é divisível por 11.
O algarismo das unidades é de 1ª ordem, o das dezenas de 2ª ordem, o das centenas de 3ª ordem, e assim sucessivamente.
Exemplos:
1) 87549
Si (soma das ordens ímpares) = 9+5+8 = 22
Sp (soma das ordens pares) = 4+7 = 11
Si-Sp = 22-11 = 11
Como 11 é divisível por 11, então o número 87549 é divisível por 11.
2) 439087
Si (soma das ordens ímpares) = 7+0+3 = 10
Sp (soma das ordens pares) = 8+9+4 = 21
Si-Sp = 10-21
Como a subtração não pode ser realizada, acrescenta-se o menor múltiplo de 11 (diferente de zero) ao minuendo, para que a subtração possa ser realizada: 10+11 = 21. Então temos a subtração 21-21 = 0.
Como zero é divisível por 11, o número 439087 é divisível por 11.
Divisibilidade por 12
Um número é divisível por 12 quando é divisível por 3 e por 4.
Exemplos:
1) 720 é divisível por 12, porque é divisível por 3 (soma=9) e por 4 (dois últimos algarismos, 20).
2) 870 não é divisível por 12 (é divisível por 3, mas não é divisível por 4).
3) 340 não é divisível por 12 (é divisível por 4, mas não é divisível por 3).
Divisibilidade por 15
Um número é divisível por 15 quando é divisível por 3 e por 5.
Exemplos:
1) 105 é divisível por 15, porque é divisível por 3 (soma=6) e por 5 (termina em 5).
2) 324 não é divisível por 15 (é divisível por 3, mas não é divisível por 5).
3) 530 não é divisível por 15 (é divisível por 5, mas não é divisível por 3).
Divisibilidade por 25
Um número é divisível por 25 quando os dois algarismos finais forem 00, 25, 50 ou 75.
Exemplos:
200, 525, 850 e 975 são divisíveis por 25.
Equações de primeiro grau
(com uma variável)
Introdução
Equação é toda sentença matemática aberta que exprime uma relação de igualdade. A palavra equação tem o prefixo equa, que em latim quer dizer "igual". Exemplos:
2x + 8 = 0
5x - 4 = 6x + 8
3a - b - c = 0
Não são equações:
4 + 8 = 7 + 5 (Não é uma sentença aberta)
x - 5 <>(Não é igualdade)
(não é sentença aberta, nem igualdade)
A equação geral do primeiro grau:
ax+b = 0
onde a e b são números conhecidos e a > 0, se resolve de maneira simples: subtraindo b dos dois lados, obtemos:
ax = -b
dividindo agora por a (dos dois lados), temos:
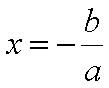
Considera a equação 2x - 8 = 3x -10
A letra é a incógnita da equação. A palavra incógnita significa " desconhecida".
Na equação acima a incógnita é x; tudo que antecede o sinal da igualdade denomina-se 1º membro, e o que sucede, 2º membro.
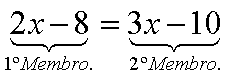
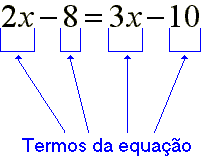
Qualquer parcela, do 1º ou do 2º membro, é um termo da equação.
| Equação do 1º grau na incógnita x é toda equação que pode ser escrita na forma ax=b, sendo a e b números racionais, com a diferente de zero. |
Pares ordenados
Muitas vezes, para localizar um ponto num plano, utilizamos dois números racionais, numa certa ordem.
Denominamos esses números de par ordenado. Exemplos:
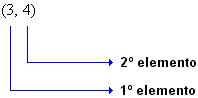
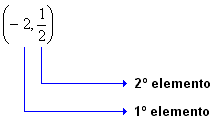
Assim:
| Indicamos por (x, y) o par ordenado formado pelos elementos x e y, onde x é o 1º elemento e y é o 2º elemento. |
-
Observações
-
De um modo geral, sendo x e y dois números racionais quaisquer, temos:
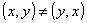. Exemplos
2. Dois pares ordenados (x, y) e (r, s) são iguais somente se x = r e y = s.
Representação gráfica de um Par Ordenado
Podemos representar um par ordenado através de um ponto em um plano.
Esse ponto é chamado de imagem do par ordenado.
Coordenadas Cartesianas
Os números do par ordenados são chamados coordenadas cartesianas. Exemplos:
A (3, 5) ==> 3 e 5 são as coordenadas do ponto A.
Denominamos de abscissa o 1º número do par ordenado, e ordenada, o 2º número desse par. Assim:
Plano Cartesiano
|
Representamos um par ordenado em um plano cartesiano. Esse plano é formado por duas retas, x e y, perpendiculares entre si. A reta horizontal é o eixo das abscissas (eixo x). A reta vertical é o eixo das ordenadas (eixo y). O ponto comum dessas duas retas é denominado origem, que corresponde ao par ordenado (0, 0). |  |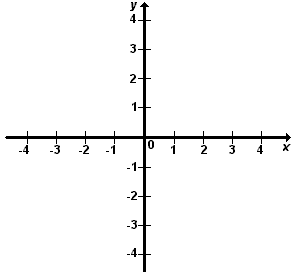
Localização de um Ponto
Para localizar um ponto num plano cartesiano, utilizamos a seqüência prática:
-
O 1º número do par ordenado deve ser localizado no eixo das abscissas.
-
O 2º número do par ordenado deve ser localizado no eixo das ordenadas.
-
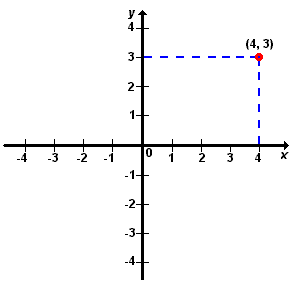
No encontro das perpendiculares aos eixos x e y, por esses pontos, determinamos o ponto procurado. Exemplo:
-
Localize o ponto (4, 3).
Produto Cartesiano
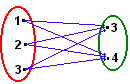
| Sejam os conjuntos A = {1, 2, 3} e B = {3, 4}. Com auxílio do diagrama de flechas ao lado formaremos o conjunto de todos os pares ordenados em que o 1º elemento pertença ao conjunto A e o 2º pertença ao conjunto B. |
|
Assim , obtemos o conjunto: {(1, 3), (1, 4), (2, 3), (2, 4), (3, 3), (3, 4)}
Esse conjunto é denominado produto cartesiano de A por B, e é indicado por:
Logo:
Dados dois conjuntos A e B, não-vazios, denominamos produtos cartesiano A x B o conjunto de todos os pares ordenados (x, y) onde
Inequações de primeiro grau
Introdução
| Denominamos inequação toda sentença matemática aberta por uma desigualdade. |
As inequações do 1º grau com uma variável podem ser escritas numa das seguintes formas:
, 
, 
, 
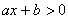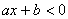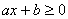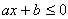, como a e b reais 
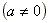. Exemplos:
 |  |  |
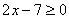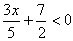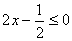Representação gráfica de uma inequação do 1º grau com duas variáveis
Método prático
-
Substituímos a desigualdade por uma igualdade.
-
Traçamos a reta no plano cartesiano.
-
Escolhemos um ponto auxiliar, de preferência o ponto (0, 0) e verificamos se o mesmo satisfaz ou não a desigualdade inicial.
Em caso positivo, a solução da inequação corresponde ao semiplano ao qual pertence o ponto auxiliar.
Em caso negativo, a solução da inequação corresponde ao semiplano oposto aquele ao qual pertence o ponto auxiliar. Exemplos:
-
Representamos graficamente a inequação
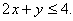
| Tabela
|  |
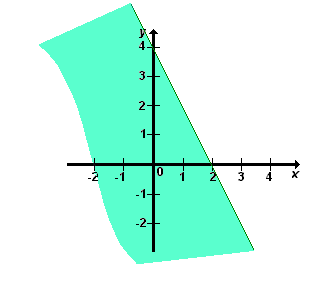Substituindo o ponto auxiliar (0, 0) na inequação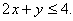
Verificamos:
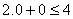
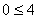(Afirmativa positiva, o ponto auxiliar satisfaz a inequação)
A solução da inequação corresponde ao semiplano ao qual pertence o ponto auxiliar (0, 0).
Radiciação
Potenciação de Radicais
Observando as potencias, temos que:
De modo geral, para se elevar um radical a um dado expoente, basta elevar o radicando àquele expoente. Exemplos:
Divisão de Radicais
Segundo as propriedades dos radicais, temos que:
De um modo geral, na divisão de radicais de mesmo índice, mantemos o índice e dividimos os radicais: Exemplos:
: 
= 
Se os radicais forem diferentes, devemos reduzi-los ao mesmo índice e depois efetue a operação. Exemplos:
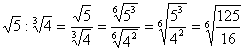
Razões - Introdução
Vamos considerar um carro de corrida com 4m de comprimento e um kart com 2m de comprimento. Para compararmos as medidas dos carros, basta dividir o comprimento de um deles pelo outro. Assim:
(o tamanho do carro de corrida é duas vezes o tamanho do kart).
Podemos afirmar também que o kart tem a metade 
do comprimento do carro de corrida.
A comparação entre dois números racionais, através de uma divisão, chama-se razão.
A razão 
pode também ser representada por 1:2 e significa que cada metro do kart corresponde a 2m do carro de corrida.
Denominamos de razão entre dois números a e b (b diferente de zero)
|
A palavra razão, vem do latim ratio, e significa "divisão". Como no exemplo anterior, são diversas as situações em que utilizamos o conceito de razão. Exemplos:
Dos 1200 inscritos num concurso, passaram 240 candidatos.
Razão dos candidatos aprovados nesse concurso:
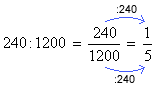(de cada 5 candidatos inscritos, 1 foi aprovado).
Para cada 100 convidados, 75 eram mulheres.
Razão entre o número de mulheres e o número de convidados:
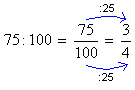(de cada 4 convidados, 3 eram mulheres).
Observações:
1) A razão entre dois números racionais pode ser apresentada de três formas. Exemplo:
Razão entre 1 e 4: 1:4 ou 
ou 0,25.
2) A razão entre dois números racionais pode ser expressa com sinal negativo, desde que seus termos tenham sinais contrários. Exemplos:
A razão entre 1 e -8 é 
.
A razão entre 
é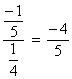 
.
Proporções - Introdução
Rogerião e Claudinho passeiam com seus cachorros. Rogerião pesa 120kg, e seu cão, 40kg. Claudinho, por sua vez, pesa 48kg, e seu cão, 16kg.
Observe a razão entre o peso dos dois rapazes:
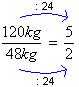
Observe, agora, a razão entre o peso dos cachorros:
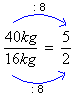
Verificamos que as duas razões são iguais. Nesse caso, podemos afirmar que a igualdade 
é uma proporção. Assim:
Proporção é uma igualdade entre duas razões.
Algarismos Romanos
A numeração romana é um sistema de numeração que usa letras maiúsculas, as quais são atribuídos valores. Os algarismos romanos são usados principalmente:
- Nos números de capítulos uma obra.
- Nas cenas de um teatro.
- Nos nomes de papas e imperadores.
- Na designação de congressos, olimpíadas, assembléias...
Regras
A numeração romana utiliza sete letras maiúsculas, que correspondem aos seguintes valores:
| Letras | Valores |
| I | 1 |
| V | 5 |
| X | 10 |
| L | 50 |
| C | 100 |
| D | 500 |
| M | 1000 |
Exemplos: XVI = 16; LXVI = 66.
Se à direita de uma cifra romana se escreve outra igual ou menor, o valor desta se soma ao valor da anterior.
Exemplos:
VI = 6
XXI = 21
LXVII = 67
A letra "I" colocada diante da "V" ou de "X", subtrai uma unidade; a letra "X", precedendo a letra "L" ou a "C", lhes subtrai dez unidades e a letra "C", diante da "D" ou da "M", lhes subtrai cem unidades.
Exemplos:
IV = 4
IX = 9
XL = 40
XC = 90
CD = 400
CM = 900
Em nenhum número se pode pôr uma mesma letra mais de três vezes seguidas. Antigamente se via as vezes a letra "I" ou a "X" até quatro vezes seguidas.
Exemplos:
XIII = 13
XIV = 14
XXXIII = 33
XXXIV = 34
A letra "V", "L" e a "D" não podem se duplicar porque outras letras ("X", "C", "M") representam seu valor duplicado.
Exemplos:
X = 10
C = 100
M = 1.000
Se entre duas cifras quaisquer existe outra menor, o valor desta pertencerá a letra seguinte a ela.
Exemplos:
XIX = 19
LIV = 54
CXXIX = 129
O valor dos números romanos quando multiplicados por mil, colocam-se barras horizontais em cima dos mesmos.
Exemplos:
Tabela de números romanos
pessoal por hooje é isso amanha e depoiis: coloca mais coisas que vcs queiram mas tbm para isso deem ideias e comentem nessa e nas outras postagens! beiijos
OBS:o assunto de amanha é Grandezas proporcionais e ....
Nenhum comentário:
Postar um comentário